Моделирование чувствительного элемента ВОД

1. Цель работы

Целью работы является ознакомление с принципом работы волоконно-оптического датчика (ВОД) магнитного поля и электрического тока, а также проведение математического моделирования чувствительного элемента (ЧЭ) ВОД магнитного поля и электрического тока.

 

2. Краткие теоретические сведения

Волоконно-оптические датчики электромагнитных полей находят всё более широкое применение в энергетике, так как позволяют эффективно решать задачи по  измерению величины тока в цепях электрических станций и линиях электропередач. Основными преимуществами волоконно-оптических датчиков являются отсутствие помех, наводимых мощными электромагнитными полями в измерительных системах на основе электрического тока, простота конструкции волоконно-оптических датчиков и их сравнительно низкая стоимость.

Однако применение различных ВОД электромагнитных полей сдерживается наличием у них относительно высокой чувствительности коэффициента преобразования датчика к температуре, обусловленной температурным дрейфом характеристик вещества чувствительного элемента.

Магнитооптическая модуляция света в кристаллах со структурой силленита (Bi₁₂SiO₂₀, Bi₁₂GeO₂₀) возникает как следствие наводимого магнитным полем H кругового двулучепреломления (эффект Фарадея), приводящего к повороту плоскости поляризации световой волны. Особенностью кристаллов Bi₁₂SiO₂₀, Bi₁₂GeO₂₀ является наличие у них естественной оптической активности Θ, поэтому угол поворота плоскости поляризации световой волны, проходящей через кристалл, будет определяться, как сумма двух слагаемых

φ=V·H·L+Θ·L,                                               (1)

где V – константа Верде Bi₁₂SiO₂₀ или Bi₁₂GeO₂₀;

H – проекция вектора приложенного магнитного поля на направление распространения световой волны в кристалле;

L – длина кристалла;

Θ – коэффициент оптической активности.

Чувствительность ВОД к магнитному полю и электрическому току определяется коэффициентом преобразования чувствительного элемента (ЧЭ), который пропорционален углу Фарадея j. Известно, что одним из способов повышения чувствительности ВОД является увеличение угла Фарадея за счет увеличения оптического пути света L в кристалле при многократном прохождении. Однако увеличение L в Bi₁₂SiO₂₀  может привести к проявлению влияния ряда нелинейных эффектов на магнитооптическую модуляцию света и коэффициент преобразования ВОД. В том числе влияния остаточного линейного двулучепреломления (ЛДП), которое всегда присутствует в Bi₁₂SiO₂₀ и определяется дефектами кристалла. Необходимо особо отметить, что предсказать величину ЛДП до изготовления кристалла возможно лишь приблизительно, а измерение этой величины достаточно трудоёмко и дорогостояще, так что является препятствием для серийного производства.

Одним из путей увеличения длины оптического пути является использование отражательной схемы построения чувствительного элемента волоконно-оптического датчика (рис.1). В этом случае используется явление взаимной компенсации влияния оптической активности за прямой и обратный проходы света в кристалле, что позволяет не учитывать её влияние и температурный дрейф оптической активности для датчиков с чётным числом проходов.

Рассмотрим математическую модель для многопроходной схемы ЧЭ (2 и более проходов). Для описания эффекта Фарадея в кристалле со структурой силленита воспользуемся формализмом матриц Джонса. Кристалл рассматривается как среда, обладающая как линейным, так и круговым двулучепреломлением. Матрица Джонса для такой среды имеет вид:

,                 (2)

где

;

C – коэффициент кругового двулучепреломления;

b - коэффициент ЛДП;

L_п – длина единичного пробега луча по кристаллу.

Для кристалла Bi₁₂SiO₂₀, Bi₁₂GeO₂₀, находящимся под воздействием магнитного поля, круговое двулучепреломление является суммой собственного кругового двулучепреломления и наведённого эффектом Фарадея:

C = Q +F,

где Q - коэффициент собственной оптической активности кристалла;

F = V×H,

где V – константа Верде;

H – проекция приложенного магнитного поля на направление распространения световой волны.

Состояние поляризации световой волны на выходе ЧЭ при линейной поляризации на входе описывается вектором Максвелла , где   – компоненты напряжённости электрического поля световой волны.

Для многопроходной схемы (рис.1а) вектор Максвелла имеет вид (для чётного и нечётного числа проходов соответственно):

 где N=2(n+1), n=0,1,2…  

(3)

 где N=1,2,3…

где

a - это угол между разрешёнными направлениями входного и выходного поляризаторов;

- матрица идеального линейного поляризатора;

R(a) – матрица поворота на угол a в двумерной прямоугольной системе координат;

M(m₁,C₁) и M(m₂,C₂) – матрицы Джонса для кристалла со структурой силленита, описывающие соответственно прямой и обратный пробеги луча света;

;   ;  ;   .

Интенсивность света I на выходе ЧЭ,  определенная как  будет представлять собой сложную функцию, зависящую от магнитного поля Н и параметров ЧЭ.

 ,                                         (4)

где L_п и N – длина одиночного пробега луча по кристаллу и число таких пробегов соответственно.

Для многопроходной схемы ВОД, вместо сетчатых поляризаторов реализующей систему «поляризатор-компенсатор» при помощи кристалла-ротатора и уголковых призм (рис.1б), вектор Максвелла имеет вид:

 где N=2(n+1), n=0,1,2…     

(5)

   где N=1,2,3…     

- матрица Джонса для кристалла-ротатора,

где L₀ – длина кристалла-ротатора.

Относительная температурная погрешность выходной интенсивности на интервале температур T₁..T₂ определяется, как

                                                          (6)

По определению коэффициент преобразования S равен:

 ,                                          (7)

Пренебрегая потерями на отражение от граней кристалла и принимая интенсивность света I₀  на входе равной 1 получаем:

.                                            (8)

Величину температурного дрейфа коэффициента преобразования ЧЭ ВОД на любом заданном интервале температур запишем, как

,                                              (9)

где T₁ и T₂ – границы интервала в ⁰С. Температурный дрейф в общем случае практически полностью определяется температурным дрейфом двух характеристик материала – собственной оптической активности Θ и константы Верде V.

Однако, как следует из уравнений (3,4,5,7,8), в случае, если ЧЭ ВОД имеет чётное число проходов, то на каждой их паре влияние собственной оптической активности взаимно компенсирует себя, и температурный дрейф коэффициента преобразования определяется только дрейфом константы Верде.

В достаточно точном приближении уравнения дрейфа характеристик материала от температуры можно принять за линейные зависимости

; ,

с различными параметрами для материалов  Bi₁₂SiO₂₀ и Bi₁₂GeO₂₀

Критичными для линейности функций (4,6,8,9) будут условия  и .  В случае несоблюдения этих условий выражения для интенсивности световой волны I на выходе кристалла и коэффициента преобразования ЧЭ становятся сложными функциями параметров кристалла и магнитного поля.

Отсюда следует, что рассмотрению в качестве изменяемых параметров модели подлежат переменные из следующего множества:

(L_n, α, β, ΔT, H),                                             (10)

а результирующими функциями модели будут переменные

(I, ΔI, S, ΔS).                                                   (11)

Тогда задачу моделирования чувствительного элемента можно определить как нахождение оптимумов функций (11) и областей распределения аргументов (10), для которых эти оптимумы существуют. То есть, речь идёт о многократном вычислении по формулам (2-9) с учётом изменения одного или нескольких параметров.

Задача нахождения оптимальных параметров такой системы трудноразрешима аналитически для числа проходов, большего двух. В этих условиях возникает необходимость прибегнуть к математическому моделированию чувствительного элемента датчика с использованием ПЭВМ.

Упрощая задачу, можно принять магнитное поле H(t) приложенным по высоте датчика, перпендикулярно зеркалам. В этом случае его проекция H в модели будет определяться, как H_п(t)=H(t)·sin(γ), где γ есть угол между направлением единичного пробега и зеркалом.

Алгоритм моделирования ЧЭ ВОД определяется уравнениями математической модели. Участие человека в моделировании сводится к заданию исходных параметров и выбору из нескольких вариантов решения оптимального по применяемым критериям.

 

3. Состав и структура средств моделирования ЧЭ ВОД

Для выполнения работы необходима ПЭВМ IBM PC, с операционной системой Windows. Программа не требовательна к размеру ОЗУ ПЭВМ, но использует значительную часть вычислительной мощности процессора. В связи с этим  рекомендуется не выполнять моделирование в фоновом режиме и использовать машины, оснащенные процессором не ниже Pentium-II с тактовой частотой 500МГц.

 

4. Выполнение

Задача 1: определить интервал приемлемой линейности выходной характеристики ЧЭ для максимального коэффициента преобразования ЧЭ при минимальной температурной погрешности ЧЭ (менее 1%). Изменяемые параметры: схема построения ЧЭ, длина единичного пробега, длина кристалла-ротатора (или угол между разрешёнными направлениями в системе "поляризатор-анализатор"). Постоянные параметры: число пробегов луча в ЧЭ, величина линейного двулучепреломления, интервал температур. Примечание: для моделирования, при котором требуется единственное значение температуры, выбирается нижняя граница интервала.

Необходимость решения задачи определяется стремлением промоделировать рабочие параметры ЧЭ и оценить его конструктивные параметры (габариты, в данном случае) для его изготовления. Линейность выходной характеристики датчика является одним из важнейших его параметров.

 

Способ решения:

1. Получить номограмму коэффициента преобразования в зависимости от изменяемых параметров. Проанализировать номограмму, сообразуясь с легендой, определить области с наивысшим коэффициентом преобразования. Сохранить графический файл, сделать необходимые заметки.

2. Получить номограмму температурного дрейфа коэффициента преобразования в зависимости от изменяемых параметров. Проанализировать номограмму, определить области с наинизшим температурным дрейфом. Сохранить графический файл, сделать необходимые заметки.

3. Определить области аргументов, в которых условия п.п. 1,2 выполняются в наилучшей степени.

4. Выбрать аргументы, принадлежащие к этой области, и получить линейный график выходной характеристики ЧЭ (зависимость выходной интенсивности от магнитного поля). Изменяя интервал аргумента, определить длину и расположение линейного участка выходного графика. Сохранить графический файл.

 

Таблица 1. Исходные данные согласно варианту                                                         

 

Результаты работы программы:

 

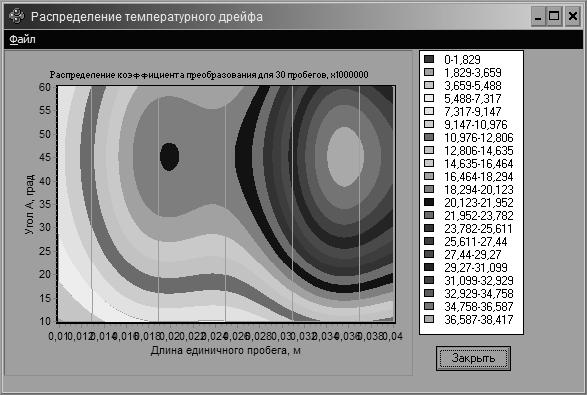
Рис. 2. Номограмма распределения коэффициента преобразования

Из анализа номограммы следует, что коэффициент преобразования уменьшается с уменьшением угла между разрешенными направлениями поляризаторов и длины единичного пробега.

 

 

 

 

 

 

 

 

 

 

 

Рис. 3. Номограмма распределения температурного дрейфа

Из анализа номограммы следует, что область приемлемых значений длины единичного пробега по условию малости дрейфа коэффициента преобразования составляет примерно 0,0155..0,0165 м (величина ΔS составляет примерно 1%) безразлично относительно величины угла между разрешенными направлениями поляризаторов. Оптимум - примерно 0,016 м (дрейф минимален, близок к нулю).

Вывод: для максимального коэффициента преобразования при минимальной температурной погрешности примерные параметры ЧЭ ВОД составят - длина единичного пробега L₀=0,016 м,  угол между разрешенными направлениями в системе «поляризатор-анализатор» α = 45⁰ .

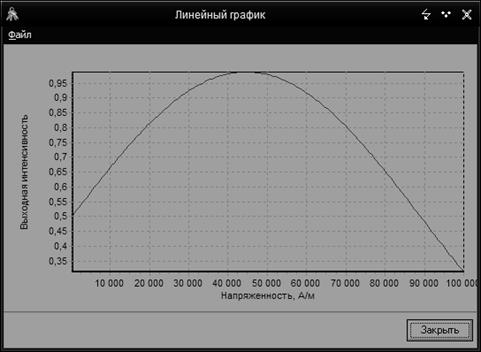
Рис. 4. Линейный график  выходной характеристики ЧЭ ВОД.

Как видно из графика, участки с приемлемой линейностью находятся примерно на интервалах аргумента 0..30000 А/м, 60000..100000 А/м.

 

Таким образом, проведено моделирование ЧЭ ВОД магнитного поля и электрического тока для заданных параметров и получено решение, позволяющее создать для указанных условий ЧЭ с максимальным коэффициентом преобразования и минимальным температурным дрейфом коэффициента преобразования, а также найдены такие интервалы величин входного сигнала, для которых не потребуется применение средств программно-аппаратной компенсации нелинейности выходной характеристики.

 

Задача 2: оценить пределы изменения линейного двулучепреломления материала кристалла ЧЭ, обладающего стабильным температурным дрейфом выходной характеристики (1%) при максимально возможном коэффициенте преобразования. Изменяемые параметры: схема построения ЧЭ, длина единичного пробега, линейное двулучепреломление. Постоянные параметры: число пробегов луча в кристалле, длина кристалла-ротатора (или угол между разрешёнными направлениями в системе "поляризатор-анализатор"), интервал температур. Примечание: для моделирования, при котором требуется единственное значение температуры, выбирается нижняя граница интервала.

 

Необходимость решения задачи определяется непредсказуемостью итоговой величины линейного двулучепреломления для известных технологий изготовления кристаллов Bi₁₂GeO₂₀, Bi₁₂SiO₂₀. Отсюда важно найти сочетание параметров ЧЭ, при котором влияние линейного двулучепреломления будет минимальным.

 

Способ решения:

1. Получить номограмму коэффициента преобразования ЧЭ в зависимости от изменяемых параметров. Проанализировать номограмму, сообразуясь с легендой, определить области с наивысшим коэффициентом преобразования, желательно возможно более стабильным относительно изменения ЛДП. Сохранить графический файл, сделать необходимые заметки.

2. Получить номограмму температурного дрейфа коэффициента преобразования в зависимости от изменяемых параметров. Проанализировать номограмму, определить области с наинизшим температурным дрейфом, а также области, в которых температурный дрейф не зависит от линейного двулучепреломления. Сохранить графический файл, сделать необходимые заметки.

3. Определить области длины единичного пробега, при которых возможно более полно выполняются условия одновременно п.п.1 и 2.

4. Выбрать несколько длин единичного пробега из этих областей и построить для них линейные графики зависимости температурного дрейфа коэффициента преобразования от величины линейного двулучепреломления, а также линейные графики зависимости температурного дрейфа выходной интенсивности от величины линейного двулучепреломления.

5. Выбрать такую длину единичного пробега, при которой температурные дрейфы выходной интенсивности и коэффициента преобразования будут минимальными. Сохранить эти графики.

 

Таблица 2. Исходные данные согласно варианту

 

Результаты работы программы:

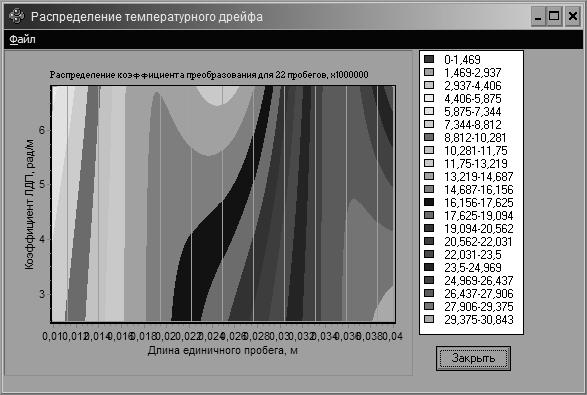
Рис. 5. Номограмма распределения коэффициента преобразования

Из анализа номограммы следует, что коэффициент преобразования ЧЭ ВОД увеличивается с увеличением длины единичного пробега и с уменьшением линейного двулучепреломления. Кроме того, заметно, что коэффициент преобразования ЧЭ ВОД более стабилен относительно изменения длины единичного пробега, чем относительно изменения величины линейного двулучепреломления.

 

Рис. 6. Номограмма распределения температурного дрейфа

Из номограммы видно, что значения температурного дрейфа, меньшие 2%, имеются на участке, определённом значениями ЛДП 2,5..6,5 рад/м и длины единичного пробега L₀=0,010 м.

 

Вывод: для минимально зависимого от ЛДП ЧЭ ВОД магнитного поля в данном случае необходимо выбрать длину единичного пробега 0,054 м (критерий: самая длинная проекция области значений, меньших 2%, на ось длины единичного пробега). При этой длине температурный дрейф коэффициента преобразования ЧЭ ВОД будет наиболее стабилен относительно ЛДП.

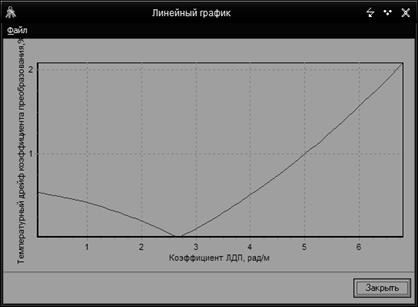
Рис.7. Зависимость температурного дрейфа от коэффициента ЛДП

Из графика видно, что величина температурного дрейфа непрерывно изменяется на всем участке изменения ЛДП. Однако, интервал изменения ЛДП, при котором температурный дрейф не превысит 1%, будет небольшим: 0..5 рад/м.