Курсовой проект по дисциплине цифровые измерительные устройства

Универсальные методы автоматической коррекции интегральной систематической погрешности ЦИУ

 

Содержание

 

1. Задание для выполнения курсового проекта.

2. Краткое описание методов автоматической коррекции:

а) Аддитивный итерационный метод автоматической коррекции;

б) Мультипликативный итерационный метод автоматической коррекции.

3. Выбор алгоритма автоматической коррекции

4. Реализация аддитивного итерационного метода коррекции погрешностей.

5. Анализ результирующей систематической погрешности.

6. Список литературы.

 

 

 

1. Задание для выполнения курсового проекта

 

Ознакомление с универсальными методами автоматической коррекции интегральной систематической погрешности цифровых измерительных устройств.

Составить алгоритм автоматической коррекции для измерительного устройства:

0 = переменный

α = 0,4

β = 0,8

 

2. Краткое описание методов автоматической коррекции

а) Аддитивный итерационный метод автоматической коррекции

Наиболее перспективными являются такие универсальные методы автоматической коррекции погрешностей, в которых высокая эффективность сочетается со сравнительной простотой технической реализации. Этим требованиям удовлетворяет метод цифровой автоматической коррекции интегральной систематической погрешности, названный итерационным, поскольку при его реализации осуществляется последовательное приближение результатов цифрового измерения к истинному значению измеряемой величины. Вычислительные операции, необходимые для реализации данного метода, заключаются в алгебраическом сложении кодов. Поэтому рассматриваемый метод был назван аддитивным итерационным методом коррекции. Измерительный процесс строится следующим образом. Производится цифровое измерение величины, результат измерения преобразуется в аналоговую величину, однородную с измеряемой, производится цифровое измерение полученной аналоговой величины, результат этого измерения вычитается из результата предыдущего измерения, и полученная разность складывается с результатом повторного цифрового измерения. В итоге получается первый скорректированный результат измерения.

Далее этот результат преобразуется в аналоговую величину, производится ее цифровое измерение, результат которого вычитается из первого скорректированного результата измерения. Затем вновь производится цифровое измерение входной величины, и результат его прибавляется к полученной ранее разности. В итоге получается второй скорректированный результат измерения.

Если обратное преобразование кода в аналоговую величину, однородную с измеряемой, производится с высокой точностью, то, как будет показано ниже, степень Коррекции систематической погрешности измерения в каждом последующем скорректированном результате практически значительно выше, чем в предыдущем. Поэтому измерительно-вычислительный процесс далее продолжается аналогично до получения скорректированного результата с необходимой точностью.

Данный способ проведения измерительного процесса может быть реализован и вручную, если в распоряжении измерителя имеется неточный, но достаточно чувствительный измерительный прибор и весовой набор образцовых мер измеряемой величины. Для автоматизации измерительно-вычислительного процесса используется точный ЦАП и автоматическое вычислительное устройство.

Обобщенная структурная схема цифрового прибора, в котором реализуется аддитивный итерационный метод автоматической коррекции погрешностей, показана на рисунке 1.

Алгоритм автоматической коррекции, при котором в каждом цикле коррекции заново производится цифровое измерение, будем называть первым аддитивным итерационным алгоритмом автоматической коррекции погрешностей или коротко АДИТЕР-1.

При реализации алгоритма АДИТЕР-1 устройство, показанное на рис.1, работает следующим образом. Первоначально измеряемая величина 0 с помощью входного переключателя Π подается на вход грубого АЦП, и происходит ее цифровое измерение. Результат измерения, выраженный в определенном коде, поступает в блок оперативной памяти БП, управляющий точным цифро-аналоговым преобразователем. На выходе ЦАП образуется аналоговая величина, однородная с измеряемой и равная результату непосредственного цифрового измерения 0.

Указанная величина с помощью переключателя Π подводится ко входу АЦП, и производится ее цифровое измерение.

Результат измерения в виде кода поступает в ВУ, где производится его вычитание из хранящегося в БП кода непосредственного цифрового измерения 0; разность Δ1 остается в БП.

Затем ко входу АЦП с помощью переключателя П вновь подводится измеряемая величина, и производится ее измерение. Результат измерения поступает в ВУ, где производится его сложение с хранящейся в БП разностью Δ1. Получается первый скорректированный результат измерения, который поступает в БП и далее подается на вход ЦАП; на его выходе образуется соответствующая аналоговая величина.

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 1. Обобщенная структурная схема прибора, реализующего аддитивный итерационный метод коррекции погрешностей

Затем выходная величина ЦАП с помощью переключателя П подается на вход АЦП, производится ее цифровое измерение, и полученный результат поступает в ВУ, где производится его вычитание из хранящегося в БП первого скорректированного результата. Получившаяся разность Δ₂ остается в БП. Затем переключатель П вновь подводит ко входу АЦП измеряемую величину, и производится ее цифровое измерение, результат которого складывается в ВУ с разностью Δ₂ , образуя второй скорректированный результат измерения. Далее работа устройства осуществляется аналогично.

Управление работой прибора осуществляется блоком управления БУ, который при необходимости также выдает скорректированные результаты измерения на цифровой индикатор ЦИ или регистратор ЦР. Поскольку в каждом последующем скорректированном результате ошибки измерения оказываются скорректированными в большей степени, чем в предыдущем, то цифровая индикация и регистрация начинаются с определенного скорректированного результата измерения в зависимости от требуемой точности, а также от значения и характера погрешности АЦП.

Самокорректирующийся прибор, реализующий алгоритм АДИТЕР-1, может работать в режимах непрерывного и разового измерений, когда измерительный процесс заканчивается с получением скорректированного результата необходимой точности.

б)  Мультипликативный итерационный метод автоматической коррекции.

Измерительно-вычислительный процесс строится следующим образом. Производится грубое цифровое измерение, его результат с помощью точного ЦАП преобразуется снова в аналоговую величину, однородную с измеряемой, производится цифровое измерение выходной величины ЦАП и определяется отношение результата цифрового измерения измеряемой величины к результату цифрового измерения вспомогательной аналоговой величины с выхода ЦАП. Умножая полученный коэффициент на результат повторного цифрового измерения измеряемой величины, получаем первый скорректированный результат измерения.

Далее этот результат с помощью ЦАП преобразуется в аналоговую величину, производится ее цифровое измерение, определяется отношение первого скорректированного результата к найденному коду, и на полученный коэффициент умножается результат следующего цифрового измерения измеряемой величины. В итоге получается второй скорректированный результат измерения. Далее при необходимости итерационный измерительно-вычислительный процесс продолжается аналогично.

Структурная схема прибора, автоматически реализующего мультипликативный итерационный метод коррекции, аналогична структурной схеме прибора, реализующего аддитивный метод (рис.1). Отличие заключается в том, что вычислительное устройство теперь вместо операций сложения и вычитания кодов осуществляет операции умножения и деления.

Алгоритм автоматической коррекции по мультипликативному методу, при котором в каждом цикле производится измерение входной величины, будем называть первым мультипликативным итерационным алгоритмом автоматической коррекции погрешностей, или сокращенно МУЛЬТИТЕР-1.

Цифровые измерительные приборы, реализующие алгоритм МУЛЬТИТЕР-1, могут работать как в режиме непрерывного измерения (МУЛЬТИТЕР-1H), так и, в режиме разового измерения, когда измерительно-вычислительный процесс заканчивается с получением скорректированного результата измерения требуемой точности (МУЛЬТИТЕР-1Р).

 

3.  Выбор алгоритма автоматической коррекции.

 

Так как b ¹ 0, то не имеет смысла применение мультипликативного метода автоматической коррекции. АДИТЕР-2 нельзя применить, так как измеряемая величина переменная. Поскольку в моём случае |g0|>1, то я считаю целесообразным использование алгоритма АДИТЕР-3, так как это позволит сократить число необходимых циклов коррекции.

 

 

 

4.  Реализация аддитивного итерационного метода коррекции погрешностей АДИТЕР-3Н

Следует отметить, что при реализации алгоритма АДИТЕР-3 самокорректирующийся цифровой прибор может работать как в режиме непрерывного измерения (АДИТЕР-ЗН), так и в режиме разового измерения (АДИТЕР-ЗР).

 

Функционально-операционная схема алгоритма АДИТЕР-3Н представлена на рис. 2. Соответствующая операционная формула имеет вид:

И1З2И3А4 З5П6И7А8 З9И10А11 З12П13И14А15З16И17А18 З19П20…

         ¯             ¯              ¯

         Р                Р                Р

где И - цифровое измерение (аналогово-цифровое преобразование);
З - запоминание; П - цифро-аналоговое преобразование, А⁺ и А^– - сложение и вычитание; Р цифровая регистрация или индикация.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.2. Функционально-операционная схема алгоритма АДИТЕР-3Н

 

5. Анализ результирующей систематической погрешности.

Результат непосредственного цифрового измерения основной измерительной цепью величины 0 может быть представлен в виде:

0  - переменная

α  = 0,4

β  = 0,8

Y₀ = 0 (1+α) + V = 1,40  + V

Для первого скорректированного результата измерения:

Y₁ = 0 (1-α²) – αV = 0,84 0 - 0,4 V

В итоге для второго скорректированного результата измерения получаем:

Y₂ = 0 (1+α³) + α² V = 1,064 0 + 0,16 V

В общем случае для  n-ого скорректированного результата измерения получаем соотношение:

Y_n = 0 [1- (-α)ⁿ⁺¹] + (-α)ⁿ V

Используя вышенаписанную формулу, получаем формулу для относительной погрешности n-ого скорректированного результата измерения

 

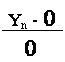
g _n =                = (-α)ⁿ (α + β) = (-α)ⁿ g_о , 

 

где β = V/0 - относительная  аддитивная составляющая погрешности основной измерительной цепи;

g_о = α + β  - относительная интегральная погрешность этой цепи.

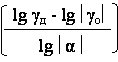
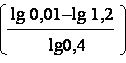Используя это соотношение, определим необходимое число циклов коррекции:

n = Ц                            = Ц                            = Ц                       = Ц(5,33) = 6,

 

где Ц – оператор округления операнда до ближайшего большего целого числа;

g_д – заданная допустимая погрешность измерения

g_д = 0,01 ;    g_о = α + β  = 1,2

Условия сходимости:

lim Y _n = 0 ;  lim g_n = 0 ;  çα ç<1

n       ∞           n       ∞

Таким образом, измерительно-вычислительный процесс является сходящимся, так как мультипликативная составляющая погрешности основной измерительной цепи меньше 100%, из этого следует, что результирующая погрешность g_n  стремится не к нулю, а определяется погрешностью ЦАП.

 

Вычисления ниже реализованы с помощью программы Microsoft Excel.

 

СПИСОК  ЛИТЕРАТУРЫ

 

1.  Алиев Т.М., Сейдель Л.Р. Автоматическая коррекция погрешностей цифровых измерительных приборов.